AtCoder Regular Contest 109参加記(~C問題)
300-400-500-0(2)-0-0でノーペナ3完1200点。
A - Hands
この問題の構造は、各階→頂点、廊下・階段→辺として重み付きグラフに落とし込める。このグラフの2頂点間の最短路問題を解けばよい。例えば、ダイクストラ法で実装すれば頂点数、辺数
より計算量は
となる。
実際に解いた時はなぜかBFSで実装していたがACできた。この辺よくわかってないのだが、最短路問題はDFSやBFSでも正しく解けるのだろうか?(今日はもう疲れたので明日考える)
B - log
長さがの丸太は、
- 長さ
の丸太そのまま
- 長さ
の丸太を切る
のどちらかの方法でしか入手できない。さらに、もし長さの丸太から長さ
の丸太を切り出せば、長さ
の丸太に関して同じ議論が続くこととなる。この時、長さが
の丸太が大量発生してもったいないので、基本的には
- 長さ
の丸太は、長さ
の丸太を買って手に入れる
ことにする。
ただし、これだと長さの丸太を有効活用できていない。どの丸太も同じ値段なのだから、はじめに長さ
の丸太を買って、短い丸太から順に切り出せるだけ切り出すのが最適である。
ここで、長さの丸太から何本の丸太を切り出せるか?という小問題が出てくる。これは、
本切り出せると仮定して二分探索を行う*1ことで
で計算可能。
から
までの整数の総和は
で求められる。
本買う予定だったうちの
本を買わずに、長さが
の丸太
本で代用するので、答えは
である。計算量は、
。
C - Large RPS Tournament
トーナメントの参加者は最大でとなるため、愚直にシミュレーションしていては当然間に合わない。ここで、各参加者が出す手は周期的であるため、同じ計算をしている箇所があるはずである。トーナメントの1回戦目を考えると、
人ごとに同じ手を出すペアが同じ順番で登場することがわかる。よって、はじめの
人分だけ考えてそれを長さ
の配列に保存すれば一回戦目の結果はすべてわかる。
その次の試合結果も、先ほどの議論を再帰的に適用することで、はじめの人分だけ考えればすべての結果がわかる。
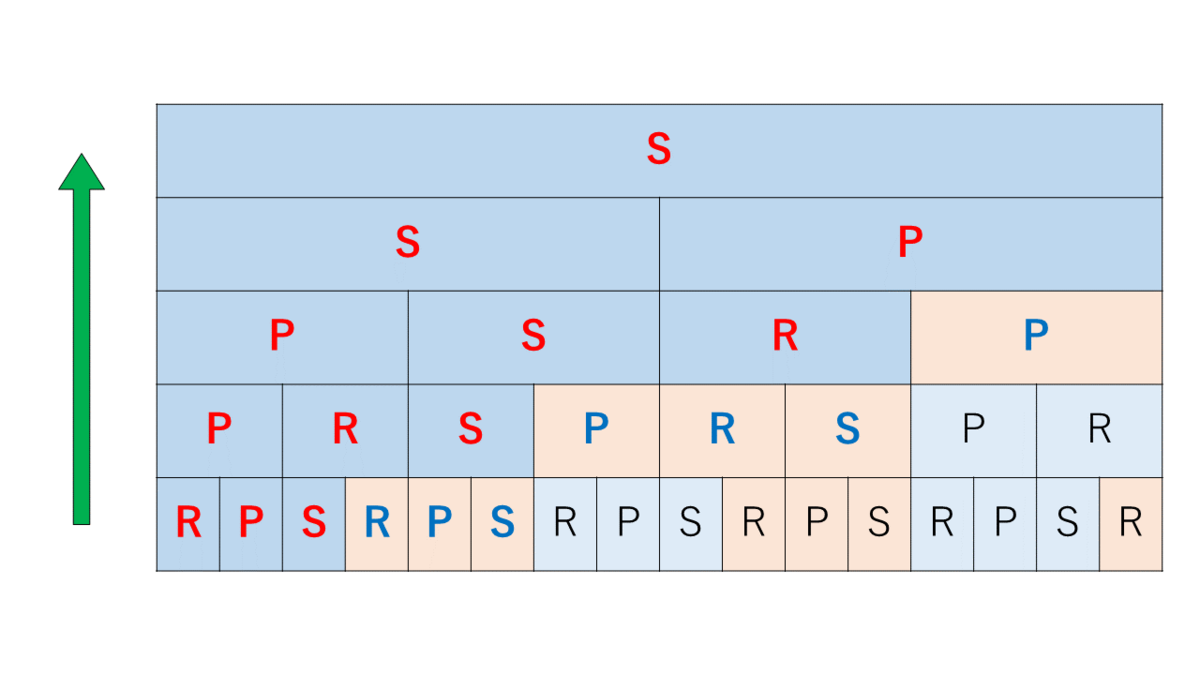
これを回繰り返したとき、配列の先頭に保存されている手が優勝する手である。
計算量は、。
D - L
解けなかった。
(諸事情により削除しました)
上記ツイートの数字は、石がそのマスまで移動するのにかかる最小手数を表している。移動したい位置がくの字であることは保証されているので、移動先の3つのマスにそれぞれ移動するまでの最小手数(上記ツイートの数字)を計算し、3つの最小手数の中の最大値に対して
- 最大値が3つ中1つだけならその最大値を出力
- 最大値が3つ中2つあるなら最大値+1を出力
というアルゴリズムで実装したが、WAだった。
感想
3完はできたものの、もう少し早くACできればもっと良かったかなと思う。ただペナルティを出さなかったのはえらい。
*1:オーバーフローを避けるために、実装時はから初めて2倍にしていく方法でやった。